Project webpage - Improving lectures in statistics

Improving Lectures in Statistics and the Use of
Computer Aided Learning and Assessment

Previous Up Next

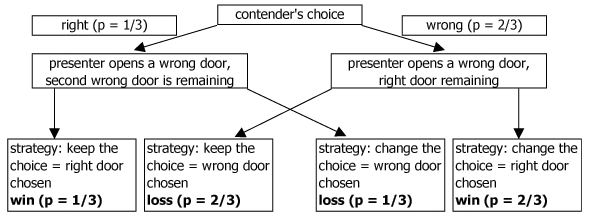
Appendix A Contest explanation

Assign value T to the event describing the choice of the correct (winning) door, and F to the event describing the choice of the door with no prize. Let be the random variable describing the first choice, the random variable describing the second choice (after presenter's hint). Without any previous hint, we have $P(X_1 = T) = \frac{1}{3}$ and $P(X_1 = F) = \frac{2}{3}$ . We are interested in the probability that the second choice will be the door concealing the prize. Then

$\displaystyle P(X_2 = T)$	$\displaystyle =$	$\displaystyle P(X_2 = T \cap X_1 = T) + P(X_2 = T \cap X_1 = F) =$
	$\displaystyle =$	$\displaystyle P(X_2 = T \mid X_1 = T)P(X_1 = T) + P(X_2 = T \mid X_1 = F)P(X_1 = F)$

If the contender is convinced about his first choice, and does not change the door, we have $P(X_2 = T \mid X_1 = T) = 1$ , and $P(X_2 = T \mid X_1 = F) = 0$ . Therefore we obtain

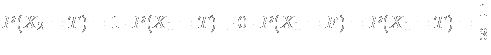
$\displaystyle P(X_2 = T) = 1\cdot P(X_1 = T) + 0\cdot P(X_1 = F) = P(X_1 = T) = \frac{1}{3}$

On the other hand, consider the situation when the contender changes his mind. Then, if he has chosen the right door with his first choice, he chooses the wrong door with his second choice (therefore $P(X_2 = T \mid X_1 = T) = 0$ ). On the contrary, if he chooses the wrong door with his first choice, then the presenter opens the second wrong door, and changing mind leads to choosing the only remaining correct door (therefore $P(X_2 = T \mid X_1 = F) = 1$ ). We obtain

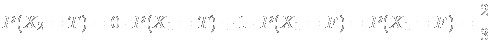
$\displaystyle P(X_2 = T) = 0\cdot P(X_1 = T) + 1\cdot P(X_1 = F) = P(X_1 = F) = \frac{2}{3}$

It makes sense for the contender to change the choice.

The above prove is schematically introduced in Figure 2.

Figure 2: Schematic tree of the contender's decision making

Top of page